Полёты 1 доллара предсказывают характер всемирной эпидемии

Популярная интернет-игра помогла учёным отследить путешествие по рукам американцев $464 тысяч в виде купюр достоинством 1 доллар. Результатом этой слежки стали статистические законы передвижения людей по Штатам и математическое описание для создания модели распространения инфекционных болезней по стране.

Как-то раз Дирк Брокманн (Dirk Brockmann), немецкий физик из института Макса Планка (Max Planck Institute for Dynamics and Self Organisation), навестил своего друга-краснодеревщика в Вермонте, и тот показал ему онлайновую игру под названием "Где Джордж?" (Where's George?).

Это развлечение некто Хэнк Эскин (Hank Eskin) придумал давно, в 1998 году. Всё довольно просто. Джордж — это Вашингтон, чей портрет украшает 1-долларовую купюру. Посетители, зарегистрировавшись на сайте, могут ввести регистрационный номер имеющейся в наличии банкноты, указать её нынешнее местонахождение и, возможно, увидеть, где эта купюра всплывала раньше — найти своего Джорджа.

Физик был заинтригован. Деньги транспортируются людьми с места на место точно так же, как и вирусы. А что, если?.. С этой идеей Брокманн отправился к коллегам — директору родного института Тео Гейзелю (Theo Geisel) и Ларсу Хафнейджелу (Lars Hufnagel) из института теоретической физики университета Калифорнии (KITP).

"Шапка" сайта игры "Где Джордж?". После сообщения об открытии учёных ресурс не справляется с наплывом посетителей (изображение с сайта wheresgeorge.ru).

В итоге трое учёных, используя 1 миллион 33 тысячи 95 сообщений от посетителей сайта, отследили перемещение по Америке 464 тысяч 670 Джорджей, проанализировали данные, развили математическую теорию и опубликовали отчёт о своей работе в журнале Nature.

"Сегодня люди перемещаются на большие расстояния за довольно короткое время, меняя при этом виды транспорта. Однако нельзя же следить за людьми как за животными с помощью маяков, тем не менее, мы должны были получить данные о движении миллионов людей, — говорит Хафнейджел. — Мы были уверены, что сможем найти на этом сайте массу любопытных данных, но результаты превзошли все наши ожидания".

Соавторы исследования из института Макса Планка: Дирк Брокманн (слева) и Тео Гейзель (фото Max Planck Institute for Dynamics and Self Organisation).

Действительно, прошли те времена, когда пандемия перемещались медленно. Это в XIV веке чуме потребовались три года, чтобы пройти европейский континент с юга на север. Средневековье люди не спешили, поэтому и чума распространялась со средней скоростью около двух километров в день.

В настоящее время международное распространение заболеваний стало серьёзной угрозой в объединённом мире интенсивной международной торговли и путешествий. Угроза птичьего гриппа и возможное появление нового "человеческого супервируса" делают прогнозирование "движения" болезней жизненно необходимым в срочном порядке.

	Третий автор работы Ларс Хафнейджел (фото Kavli Institute for Theoretical Physics).

"Таким образом, мы вправе ожидать, что будущие пандемии распространятся по другим правилам, с куда большей скоростью. И атипичная пневмония нам уже это продемонстрировала", — указывает Хафнейджел.

Авторы работы говорят, что передвижения людей соответствуют тому, что математики называют универсальным масштабом, и согласуются с правилами степенной зависимости.

Но больше всего учёных удивило то, что распространение купюр определяется всего двумя универсальными параметрами – двумя аномальными путями "рассеивания".

Во-первых, это случайное блуждание, известное как полёты Леви (Lйvy flight). Журнал New Scientist объясняет их так: притом, что большинство банкнот всякий раз путешествует на небольшие расстояния, есть небольшая вероятность, что купюры вдруг "прыгнут" очень далеко, например, улетят в бумажнике авиапассажира.

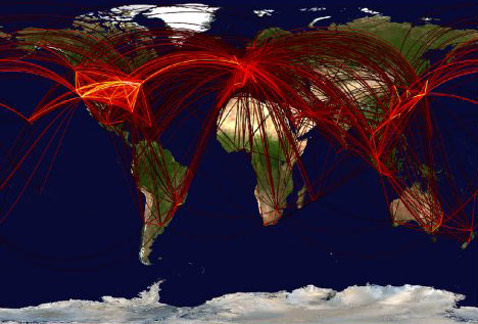Используемая учёными всемирная сеть воздушных сообщений между 500 крупнейшими аэропортами Земли. Чем ярче цвет, тем загруженнее линия (изображение Max Planck Institute for Dynamics and Self Organisation).

Во-вторых, это "хвосты" кривой распределения вероятностей. По New Scientist, это означает шанс, что банкноты будут оставаться в одном месте в течение долгого времени, скажем, попадут в копилку ребёнка.

Вот, как бы, и всё. Этого, по мнению авторов исследования, достаточно, чтобы вычислить вероятность того, что банкнота преодолеет определённое расстояние в определённое время. Учёные пишут:

"Мы показали, что поведение путешественников может быть с удивительной точностью описано математически в пространственно-временном масштабе с двумя параметрами модели случайного блуждания, и заключили, что путешествия людей в географическом масштабе — противоречивый и эффективно супердиффузный процесс".

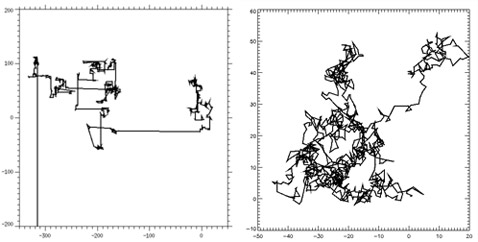Примеры случайного блуждания, названного полётами Леви в честь французского математика (иллюстрации с сайта wikimedia.org).

Брокманн, правда, признаёт, что распространение денег, возможно, в совершенстве не отражает передвижения людей, однако, говорит, что сравнение модели с доступной информацией относительно пассажирских авиаперелётов и дорожных путешествий показывает, что всё точно.

А директор института Макса Планка заявил: "Мы с оптимизмом полагаем, что наше исследование значительно улучшит качество прогнозов географического распространения эпидемий". Очень хорошо, если так.

Другие сообщения раздела Новости науки